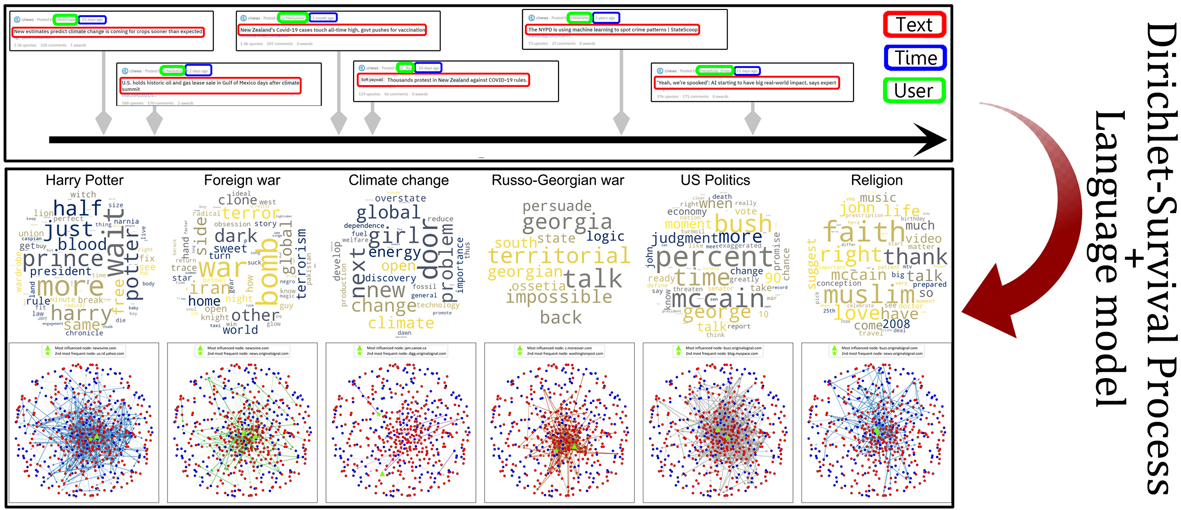
Dirichlet-Survival Process - Scalable Inference of Topic-Dependent Diffusion Networks
Information spread on networks can be efficiently modeled by considering three features: documents’ content, time of publication relative to other publications, and position of the spreader in the network. Most previous works model up to two of those jointly, or rely on heavily parametric approaches. Building on recent Dirichlet-Point processes literature, we introduce the Houston (Hidden Online User-Topic Network) model, that jointly considers all those features in a non-parametric unsupervised framework. It infers dynamic topic-dependent underlying diffusion networks in a continuous-time setting along with said topics. It is unsupervised; it considers an unlabeled stream of triplets shaped as (time of publication, information’s content, spreading entity) as input data. Online inference is conducted using a sequential Monte-Carlo algorithm that scales linearly with the size of the dataset. Our approach yields consequent improvements over existing baselines on both cluster recovery and subnetworks inference tasks.
Reference:
Dirichlet-Survival Process - Scalable Inference of Topic-Dependent Diffusion Networks
G. Poux-Médard, J. Velcin, S. Loudcher, ECIR, 2023